[ASAC] CNN
제안 : 전통적인 이미지 특징 + 인공 신경망 => Filter 시용해서 Feature Map 사용

풀링은 사이즈 이미지 사이즈만 바꾸는것
C3 : 6개 로 들어가고 / 이 3x3x6 짜리가 16개 있어야한다
피처맵 이후는 분류 네트워크 DNN
Flatten 전까지는 필터를 통해서 이미지의 특정을 추출하자!
인공 신경망이 알아서 해주는거 아니야? No no 수치들을 뽑아내는거지 실제로는
이미지의 특징을 추출해야한다.
콘벨루션이라는 연산을 활용해서 이미지의 특징을 추출
ConV / sampling
차원을 잘 봐야함
CNN
- Convolution이란? -
• Convolution
• 두 함수를 곱해서 적분하는 연산
• 함수 f에 다른 함수 g를 적용해서 새로운 f_new를 만들 때 사용.


CNN
- Image에서 Convolution이란? -
• 앞의 convolution 연산이 이미지에서 어떠한 역할을 하는지에
대해서 보면
• 특징 추출 : 세로 특성 , 가로 특성, edge추출 등
• 이미지 변환 : 뿌옇게 하는 현상,
-> 전통적인 이미지에 Filter를 적용하는 방식임!!!

필터 -> 어떤 특징을 추출할꺼냐?

행렬을 사용
이미지가 뭉개지는것을 막고자 항등행렬과 차이를 보이게 만듬





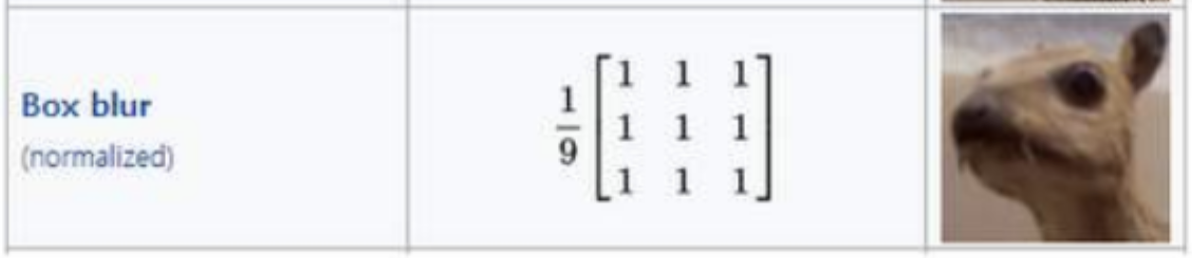
이미지를 뭉개서 사용하는 블러처리!
어떤 필터를 쓰느냐에 따라서 값이 달라지기 떄문에, 예전에는 필터가 더 중요했음!
내부적으로는 행렬의 곱
그래서 다양한 필터를 쓰면 뭐가 좋은데???
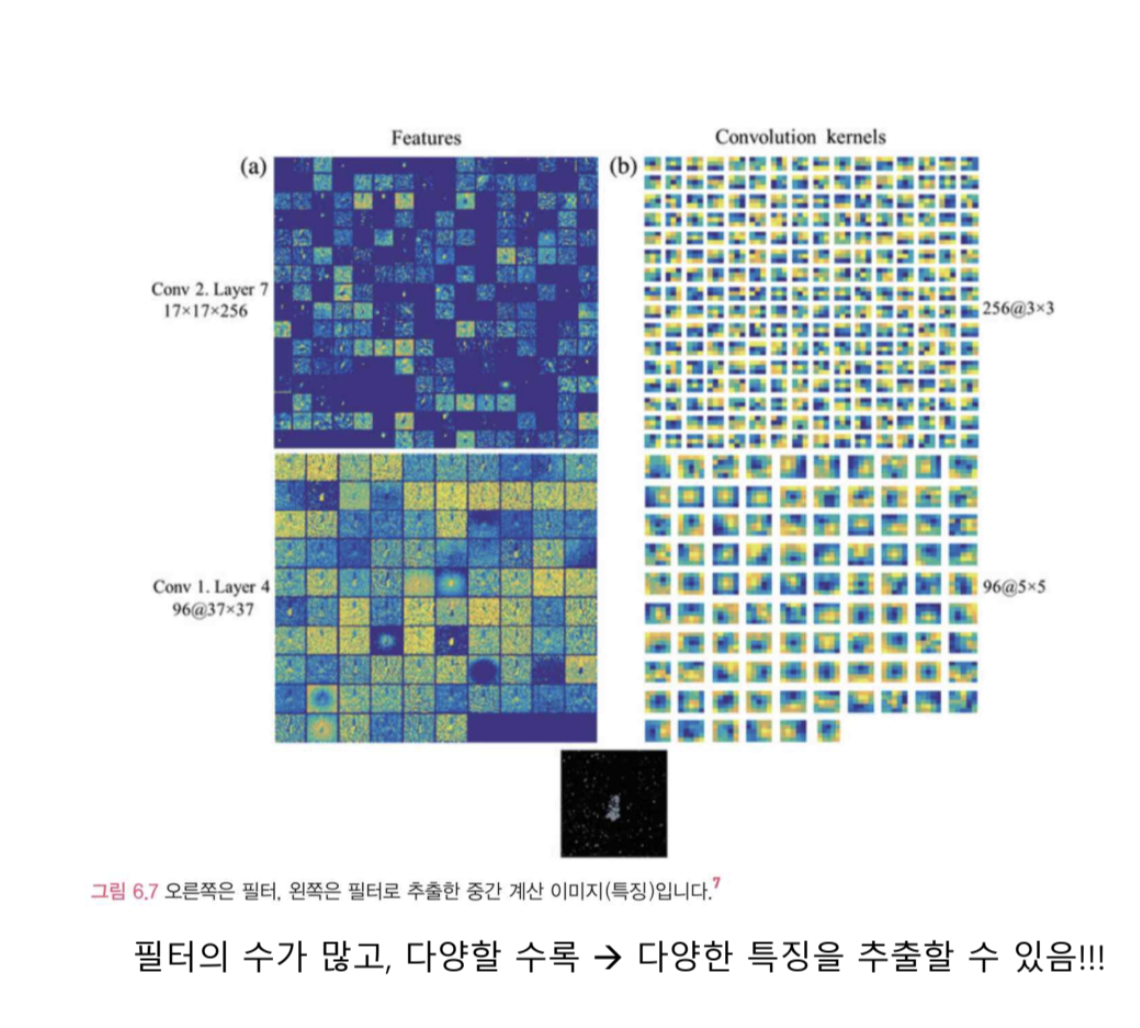
풍부한 재료들을 바탕으로 좋은 특징과 많은 재료들을 얻을수가 있다.
딥러닝은 설명보다는 성능에 초첨!
필터와 컨벌루션 연산의 의미를 알아야한다!
그래서 CNN이 뭔데?
두개의 함수를 곱한뒤에 누적(적분을 시킨다!)
선형 결합(線型 結合, linear combination) 또는 일차 결합(一次 結合)은 수학에서 각 항에 상수를 곱하고 결과를 더함으로써 일련의 항으로 구성된 표현식이다(예: x와 y의 선형 결합은 ax + by 형식인데 여기서 a와 b는 상수이다) 선형 결합의 개념은 선형대수학과 수학 관련 분야의 중심이다. 이 글의 대부분은 체 위의 벡터 공간의 맥락에서 선형 결합을 다루며 글의 끝에 주어진 일부 일반화를 다룬다.
LC -> 인공 신경망
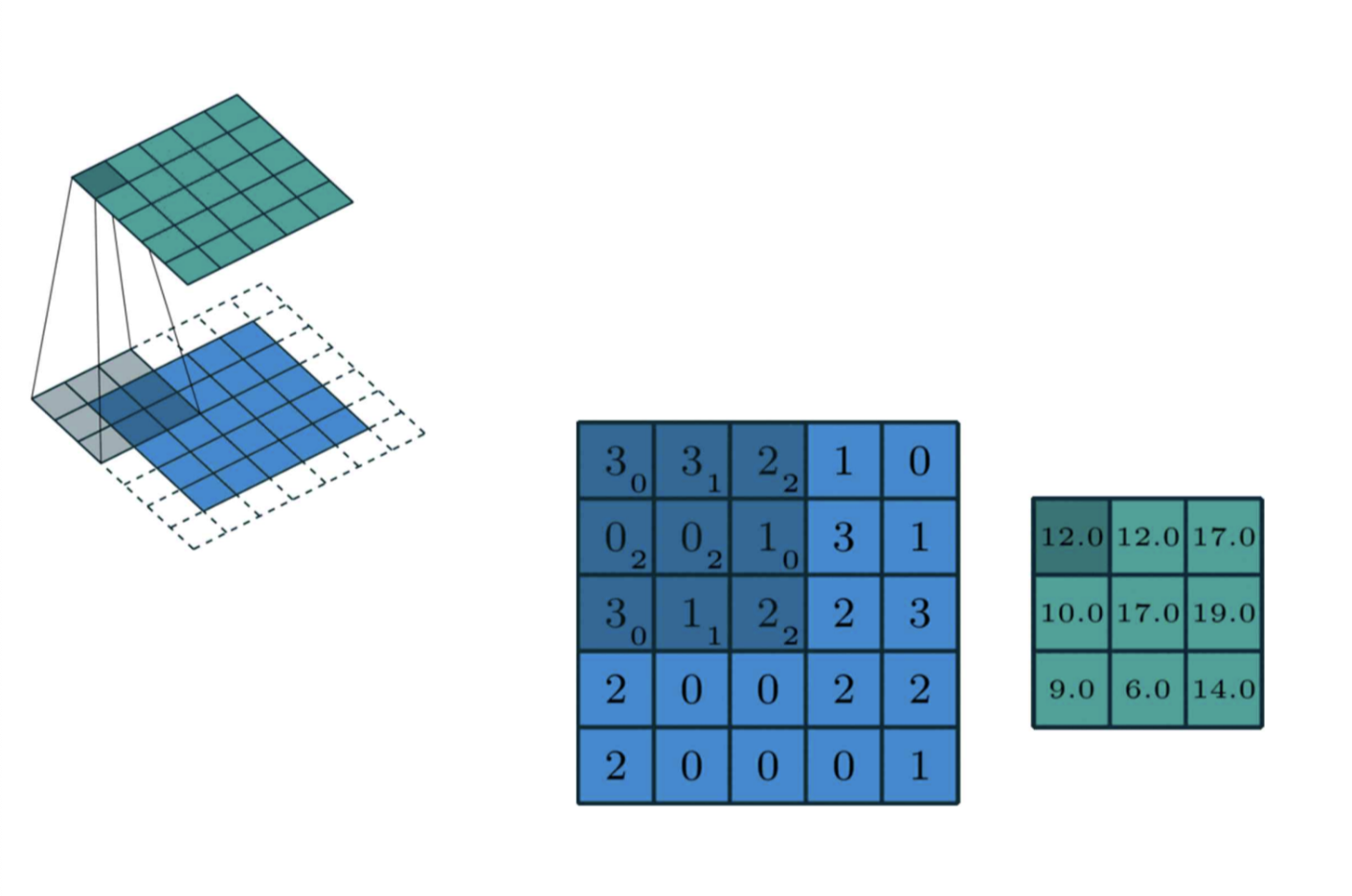
이렇게 한판씩 밀어서 한칸에 Scalar 값으로 이미지의 특징이 담긴다!
CNN
- 입력 데이터 Shape -
• 이미지 데이터는 2D가 아니라 3D 데이터임!! -> 3D Tensor!!!
Conv -> 이미지
컬러 이미지 3차원 / 컬러 이미지 셋이 쌓여 있다면 4차원
컬러 => 3채널
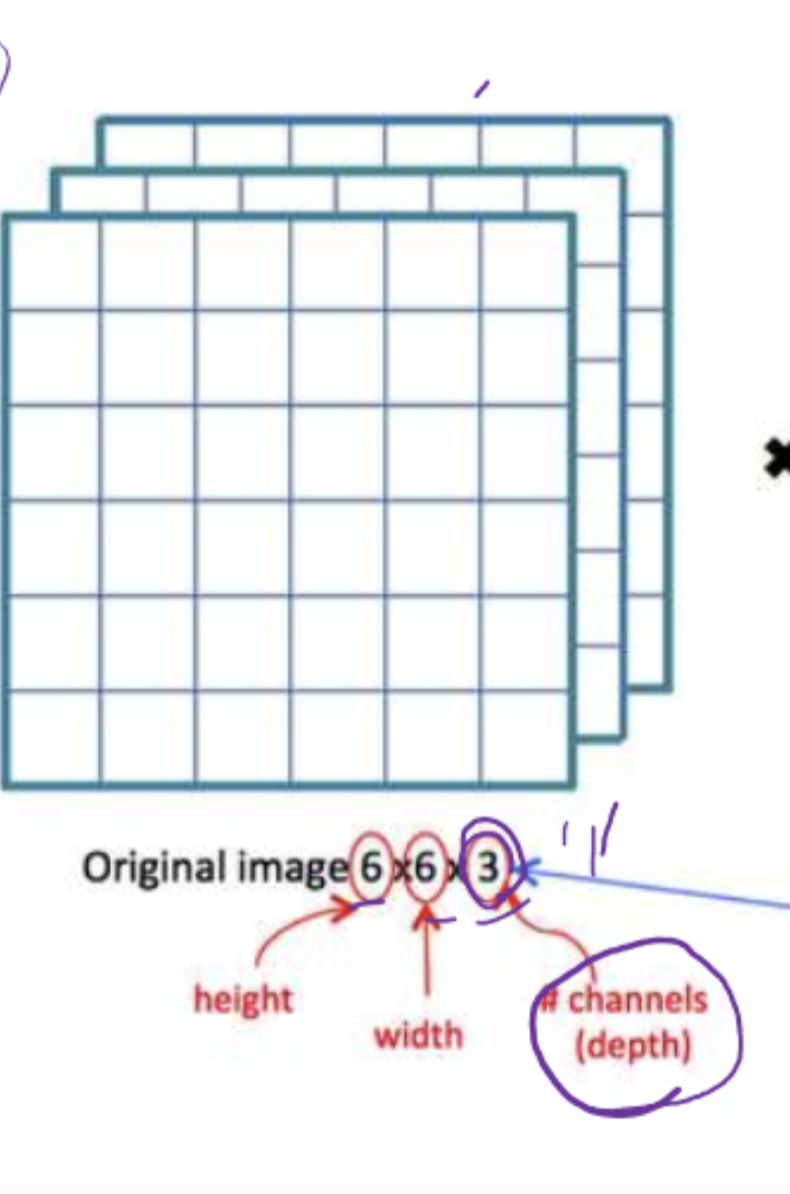
여기서 CONV2에서는 이미지의 채널을 신경쓰지 않고, 필터의 크기 즉, 2d만 인식하고 채널의 갯수는 생각하지 않는다!



필터 1개 -> 필터맵 1장
6x6 과3x3이 무엇을 결정하냐 나오는 피처맵의 사이즈
CNN
- Conv Filter의 Size & numbers? -
• 뉴런의 수용 영역은 Conv Filter의 Size에 따라서 달라진다.
• 모든 Layer에서 작은 size의 Conv Filter를 사용: 수용 영역을 조금씩 늘려가면서 특징을 학습하게 됨.
• 모든 Layer에서 큰 size의 Conv Filter를 사용: 수용 영역을 빠르게 확장하며 특징을 학습하게 됨.
• Conv Filter의 Size에 따라서 신경망의 성능이 달라짐 -> Conv Filter Size는 신경망의 성능이 최대가 되도록 설정해야 한다!!! à 일반적으로 3 by 3, 5 by 5, 7 by 7 등의 크기를 사용함!!!
• Conv Filter의 numbers : 이미지의 복잡도에 따라서 달라짐. -> 각기 Conv Filter는 다른 특징을 학습을 하기 때문에 이미지의 특징이 다양할 수록 더 많이 필요하게 됨.
CNN
- 표준 Conv 연산 -
• 이미지 데이터가 가지고 있는 3D의 특성을 반영을 하여서, 모든
Channel에 대한 값을 한 번에 가중합산을 한다. -> 최종 1번 연산에서 1개의 스칼라 값이 나온다!!!!

- Padding

CONV 하게 되면 이미지가 줄어듬, 이걸 보정하기 위해 원본 테투리에 0을 쳐줌,
Feature 맵의 사이즈를 원본이랑 유지하기 위해

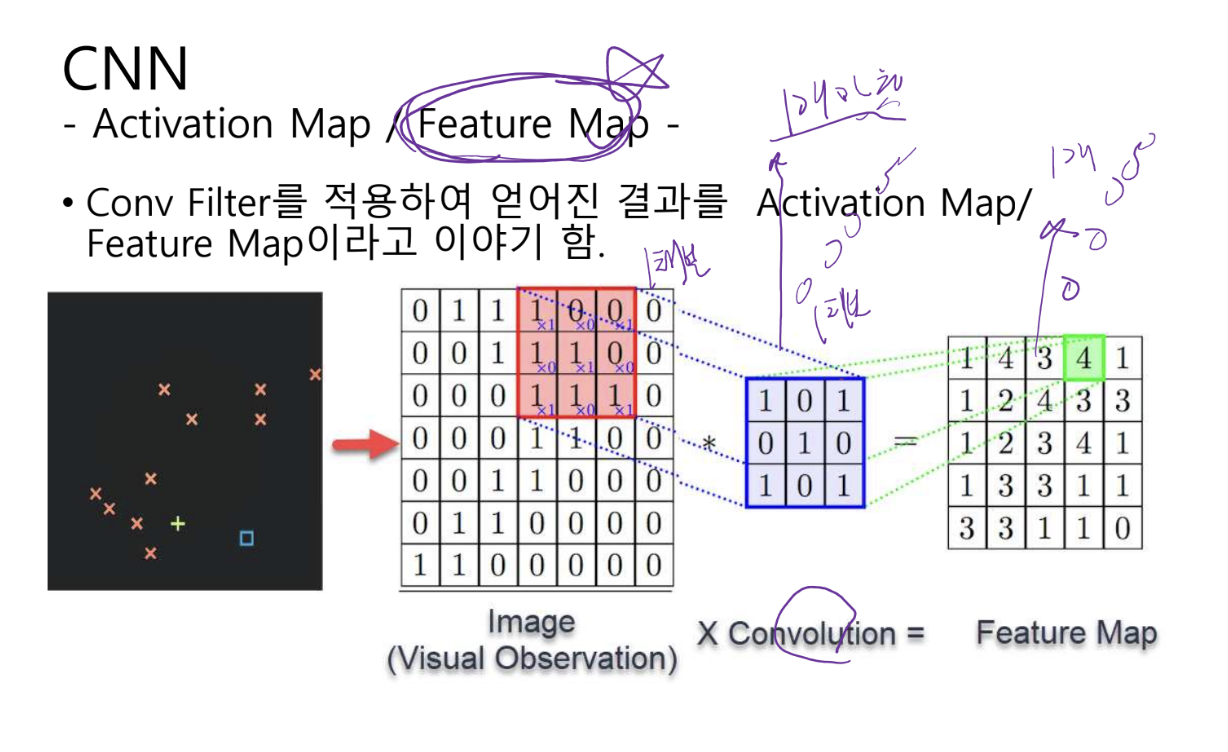
X Convolution이 weight라는것을 인식! 가운데 파란색!

피처의 채널수는 = 필터의 갯수!
