| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| 30 |
- ㅂ.
- ai 새싹 부트캠프 5일차
- 새싹 AI데이터새싹 엔지니어 부트캠프 1일차
- Til
- ai 새싹 부트캠프 6일차
- 통계용어 정리
- 데이터분석가
- T
- X
- 취준생
- 새싹 AI데이터새싹 엔지니어 부트캠프
- ai 새싹 부트캠프 4일차
- 데이터관련면접
- 데이터분석가면접준비
- ai 새싹 부트캠프 7일차
- 새싹 AI데이터새싹 엔지니어 부트캠프 3일차
- ASAC
- 새싹 AI데이터새싹 엔지니어 부트캠프 2일차
- Today
- Total
데이터 공부기록
[Algorithm] Before KNN 본문
KNN classification - Fundamentals
- Measures of similarity
1) Euclidean distance
2차원의 점의 거리를 구하는 방법으로

피타고라스의 정리에서 '대각선'구하는 공식을 사용한다. 구하려는 값을 뺸후의 제곱하여 루트를 씌워서 쓴다.
ㄱ. IN MATH


ㄴ. Code in Python
def euclidean_distance(pt1, pt2):
distance = 0
for i in range(len(pt1)):
distance += (pt1[i] - pt2[i]) ** 2
return distance ** 0.5
# print(euclidean_distance([5, 4, 3], [1, 7, 9]))
2) Manhattan distance
Manhattan distance 도 Euclidean distance 와 유사하지만,

각 차원의 차를 제곱해서 사용하는 게 아니라. 바로 그냥 절대값을 바로 합산하는 거다. (대각선을 이용하지 않기 떄문에)
아래 그림에서 처럼 대각선을 이용하지않고, 최단 거리를 간다고 이해하면 된다. (a에서 b로 이동할 때 몇 칸씩 이동하는지 생각하자.)
또한, 앞서 설명한 것 처럼 대각선을 이용하지않기 떄문에, Manhattan distance 는 Euclidean distance보다 항상 크거나 같다.
(Manhattan distance >= Euclidean distance)
ㄱ. IN MATH
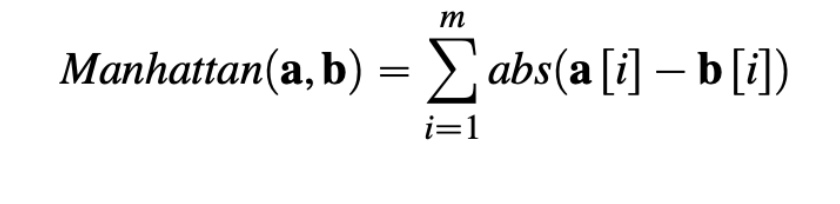

ㄴ. Code in Python
def manhattan_distance(pt1, pt2):
distance = 0
for i in range(len(pt1)):
distance += abs(pt1[i] - pt2[i])
return distance
Distance Metrics

Euclidean(d12, d5) = 5.4829 Manhattan(d12, d5) = 7.25
Euclidean(d12, d17) = 7.0044 Manhattan(d12, d17) = 7.25
유클리드 거리(Euclidean distance)는 여러 특성에서 발생하는 작은 차이보다는 한 특성에서의 큰 차이에 더 큰 영향을 받습니다.
∙ Decision boundary
∙ boundary between regions of the feature space
in which different target levels will be predicted. ∙ k =1
∙ Advantages
∙ relatively straightforward to update the model
when new labeled instances become available. ∙ k =1
∙ Handling Noisy Data
∙ k-nearest neighbors algorithm ∙ k =3
∙ Handling Noisy Data
∙ k-nearest neighbors algorithm ∙ k =5 /
적절한 k 값을 찾는 것이 중요!
∙ Handling Noisy Data
∙ k-nearest neighbors algorithm ∙ k = 15
∙ Weighted k-nearest neighbors algorithm ∙ k = 21
'sesac ai 과정 > Algorithm' 카테고리의 다른 글
| [algorithm] bayes 베이즈 정리 (0) | 2023.10.20 |
|---|---|
| [Bayes' Theroem] : UPDATE (0) | 2023.10.17 |
| [Algorithm - Decision Tree] - about information entrop (0) | 2023.10.12 |
| [Algorithm 공부법] (0) | 2023.10.12 |
| [Algorithm - Decision Tree] - (Classification & Regression,Fundamentals, Entropy) (0) | 2023.10.12 |



